Площ на кръг: формула. Защо площта на описания и вписан в квадрат кръг е равна на правоъгълен равнобедрен триъгълник, правоъгълен равнобедрен трапец?

Как да намерим площта на кръг? Първо намерете радиуса. Научете се да решавате прости и сложни задачи.

Окръжността е затворена крива. Всяка точка от кръговата линия ще бъде на еднакво разстояние от централната точка. Кръгът е плоска форма, така че решаването на задачата за намиране на площта е лесно. В тази статия ще разгледаме как да намерим площта на кръг, вписан в триъгълник, трапец, квадрат и описан близо до тези фигури.

Площ на кръг: формула, използваща радиус, диаметър, дължина на кръг, примери за решаване на проблеми

За намиране на площта на ​​фигура, трябва да знаете, че такива са радиусът, диаметърът и числото π.

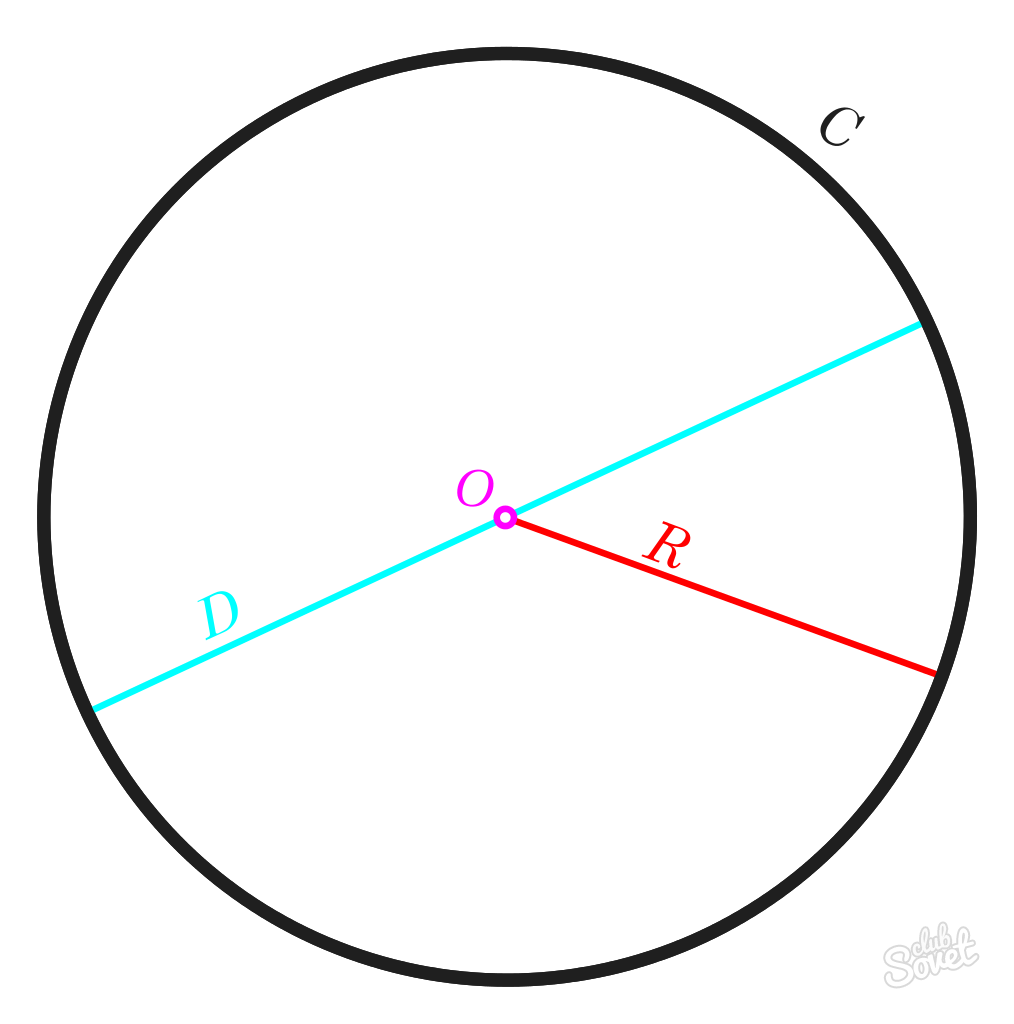
Радиус R е разстоянието, ограничено от центъра на окръжността. Дължините на всички R-радиуси на една окръжност ще бъдат равни.

Диаметър D е линия между произволни две точки от окръжност, минаваща през централната точка. Дължината на този сегмент е равна на дължината на R-радиуса, умножена по 2.

Числото π е постоянна стойност, равна на 3,1415926. В математиката това число обикновено се закръгля до 3,14.

Формулата за намиране на площта на окръжност през радиуса:

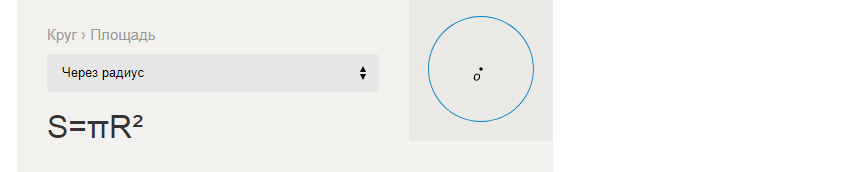
Примери за решаване на задачи за намиране на S-областта на окръжност през R-радиуса:

---------- ---------------------------- --

Задача: Намерете лицето на кръг, ако радиусът му е 7 cm.

Решение: S=πR2, S=3,14*72, S=3,14*49=153,86 cm2.

Отговор: Площта на кръг е 153,86 cm2.

Формулата за намиране на S-площта на окръжност през D-диаметър:

Примери за решаване на задачи за намиране на S, ако D е известно:

--------- --------------------------------

Мисия: Намерете S на окръжност, ако D е равно на 10 cm.

Решение: P=π*d2/4, P=3,14*102/4=3,14*100/4=314/4=78,5 cm2.

Отговор: Площта на плоска кръгла фигура е 78,5 cm2.

Намиране на S на окръжност, ако дължината на окръжността е известна:

Първо намираме какъв е радиусът. Дължината на окръжността се изчислява по формулата: L=2πR, съответно радиусът R ще бъде равен на L/2π. Сега намираме площта на кръга, използвайки формулата чрез R.

Нека разгледаме решението на примера на проблема:

----------- -----------------------------

Задача: Намерете лицето на окръжност, ако е известна дължината на окръжността L — 12 cm.

Решение: Първо намираме радиуса: R=L/2π=12/2*3.14=12/6.28=1.91.

Сега намираме площта през радиуса: S=πR2=3,14*1,912=3,14*3,65=11,46 cm2.

Отговор: Площта на кръг е 11,46 cm2.

Площ на кръг, вписан в квадрат: формула, примери за решаване на задачи

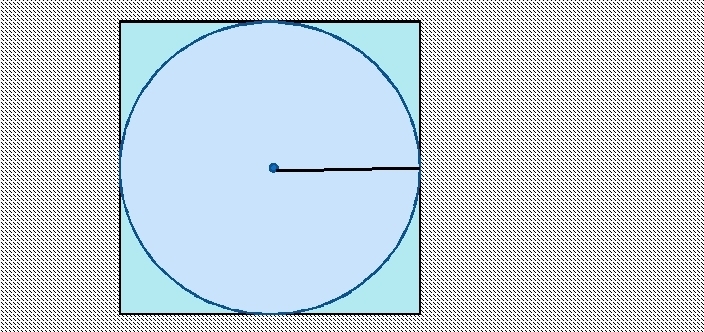
Намирането на площта на окръжност, вписана в квадрат, е лесно. Страната на квадрата е диаметърът на кръга. За да намерите радиуса, трябва да разделите страната на 2.

Формулата за намиране на площта на кръг, вписан в квадрат:

Примери за решаване на задачи за намиране на площта на окръжност, вписана в квадрат:

-- ---------------------------------- ----

Задача № 1: Известна е страната на квадратна фигура, която е равна на 6 сантиметра. Намерете S-областта на вписания кръг.

Решение: S=π(a/2)2=3,14(6/2)2=3,14*9=28,26 cm2.

Отговор: Площта на плоска кръгла фигура е 28,26 cm2.

----------------------------------------------- -----------

Задача #2 :Намерете S на окръжност, вписана в квадратна фигура и неговият радиус, ако едната страна е равна на a=4 вижте

Решете както следва : Първо намираме R=a/2=4/2=2 вж.

Сега ще намерим площта на кръга S=3.14*22=3.14*4=12.56 cm2.

Отговор: Площта на плоска кръгла фигура е 12,56 cm2.

Площ на окръжност, описана около квадрат: формула, примери за решаване на задачи

Малко по-трудно е да се намери площта на кръгла фигура, описана около квадрат. Но, знаейки формулата, можете бързо да изчислите тази стойност.

Формула за намиране на S на окръжност, описана около квадратна фигура:

Примери за решаване на задачи за намиране на площта на кръг, описан около квадратна фигура:

Задача

Площ на окръжност, вписана в правоъгълен и равнобедрен триъгълник: формула, примери за решаване на задачи

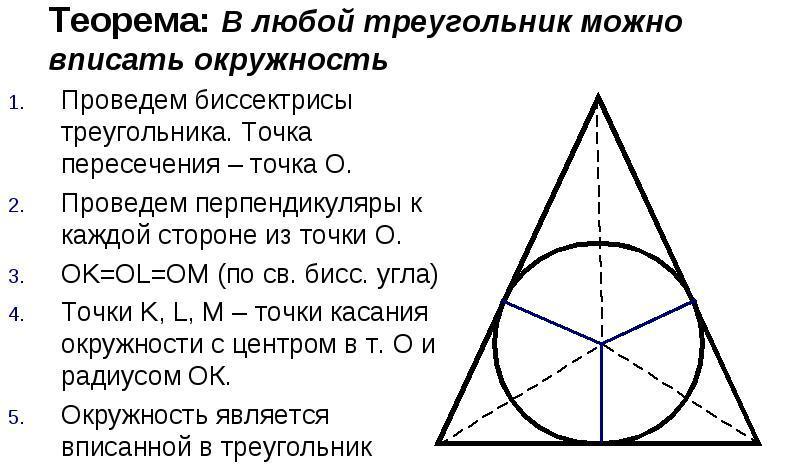
Окръжност, вписана в триъгълна фигура, е окръжност, която се допира до трите страни на триъгълника. Всяка триъгълна фигура може да бъде вписана с кръг, но само един. Центърът на окръжността ще бъде точката на пресичане на ъглополовящите на триъгълника.

Формула за намиране на площта на окръжност, вписана в равнобедрен триъгълник:

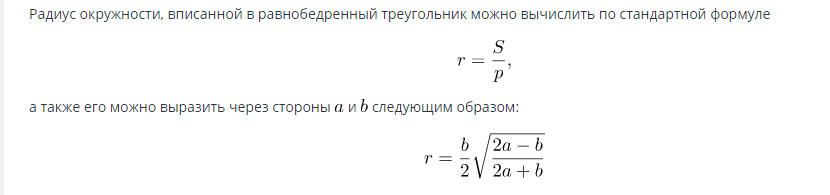
Когато радиусът е известен, площта може да се изчисли по формулата: S=πR2.

Формула за намиране на площта на окръжност, вписана в правоъгълен триъгълник:

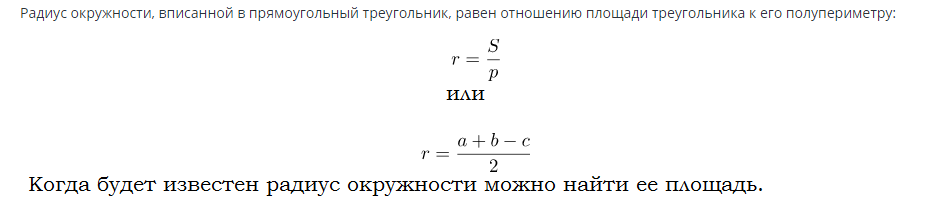
Примери за решения на задачи:

Задача # 1

)

Ако в тази задача трябва да намерите и площта на кръг с радиус 4 cm, тогава можете да го направите по формулата: S=πR2

Задача №2

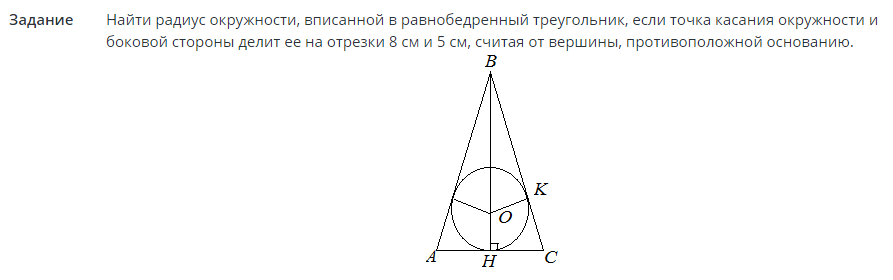
Решения:

Сега, когато радиусът е известен, площта на кръга може да се намери по отношение на радиуса. Вижте формулата по-горе в текста.

Задача #3

Площ на окръжност, описана около правоъгълен и равнобедрен триъгълник: формула, примери за решаване на задачи

Всички формули за намирането на площта на кръг се свежда до факта, че първо трябва да намерите неговия радиус. Когато радиусът е известен, тогава намирането на площта е лесно, както е описано по-горе.

​​​​

Площта на окръжност, описана около правоъгълен и равнобедрен триъгълник, се намира по следната формула:

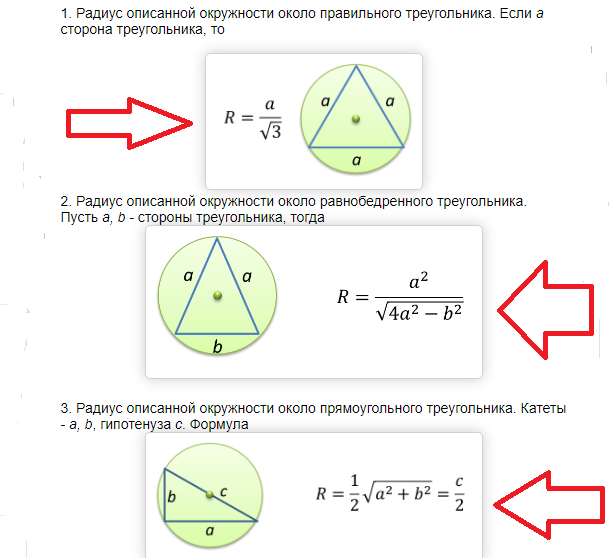
Примери за решаване на задачи:

Ето още един пример за решаване на проблем при използване на формулата на Heron.

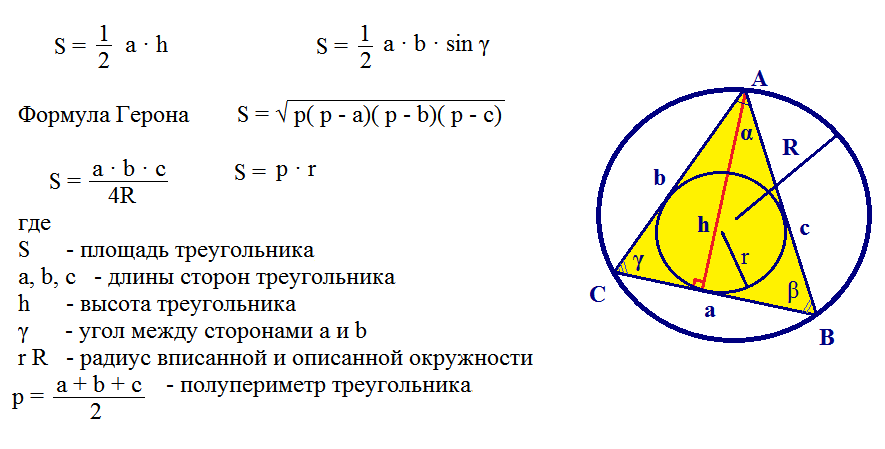
Трудно е за решаване подобни проблеми, но те могат да бъдат преодолени, ако знаете всички формули. Такива задачи решават учениците в 9. клас.

Площ на окръжност, вписана в правоъгълен и равнобедрен трапец: формула, примери за решаване на задачи

Например, равнобедрен трапец е вписан с кръг, който е в точката на контакт, разделя едната страна на сегменти m и n.

За да разрешите този проблем, трябва да използвате следните формули:

Намирането на площта на кръг, вписан в правоъгълен трапец, се извършва по следната формула:

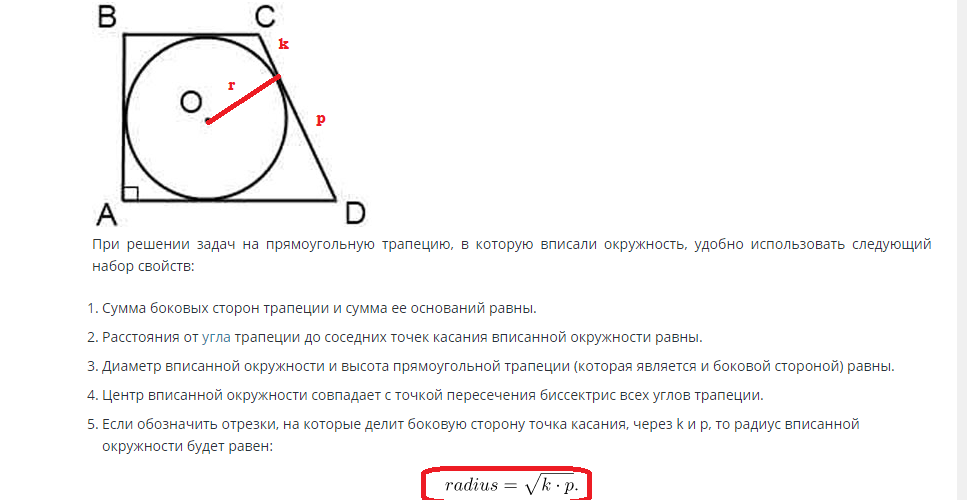
Ако страната е известна, тогава радиусът може да се намери чрез тази стойност. Височината на страната на трапеца е равна на диаметъра на кръга, а радиусът е половината от диаметъра. Съответно радиусът е равен на R=d/2.

Примери за решаване на задачи:

Площ на окръжност, описана около правоъгълен и равнобедрен трапец: формула, примери за решаване на задачи

Трапецът може да бъде вписан в окръжност, когато сборът от срещуположните ъгли е 180°. Следователно може да се впише само равностранен трапец. Радиусът за изчисляване на площта на окръжност, описана в близост до правоъгълен или равнобедрен трапец, се изчислява по следните формули:

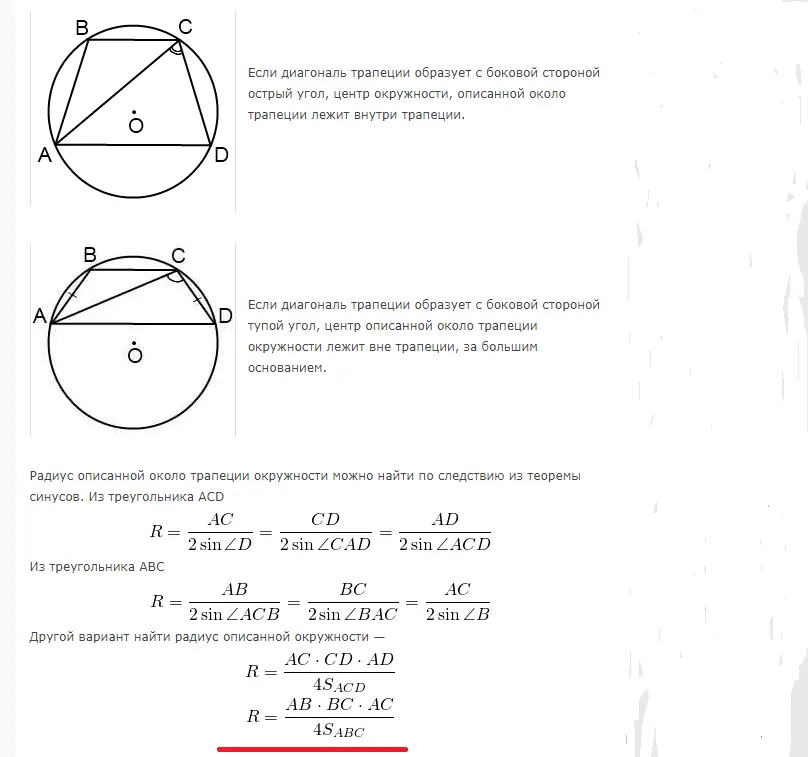
Примери за решаване на задачи:

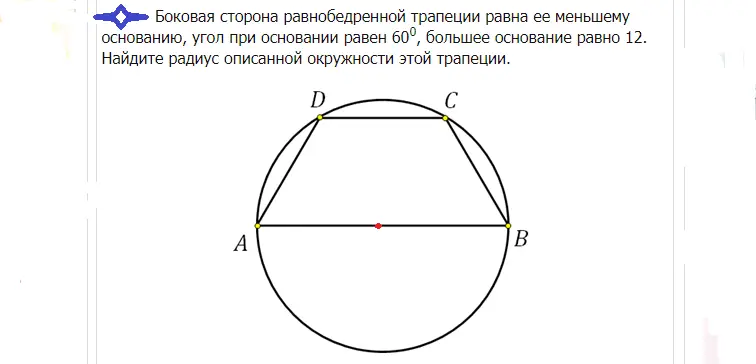
Решение: Голямата основа в този случай минава през центъра, тъй като в окръжността е вписан равнобедрен трапец. Центърът разделя тази основа точно наполовина. Ако основата AB е равна на 12, тогава радиусът R може да се намери, както следва: R=12/2=6.

Отговор: Радиусът е 6.

В геометрията е важно да се знаят формулите. Но е невъзможно да запомните всички, така че дори на много изпити е позволено да използвате специален формуляр. Важно е обаче да можете да намерите правилната формула за решаване на този или онзи проблем. Практикувайте решаването на различни задачи за намиране на радиус и площ на кръг, за да можете правилно да замествате формули и да получавате точни отговори.

Видео: Математика | Изчисляване на площите на кръг и неговите части